截對角偏方面體
外观
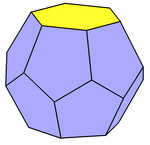
 以正十二面體作為截對角五方偏方面體為例 | |
| 類別 | 截對角偏方面體 |
|---|---|
| 對偶多面體 | 雙錐反柱體 |
| 性質 | |
| 面 | |
| 邊 | |
| 頂點 | |
| 歐拉特徵數 | F=, E=, V= (χ=2) |
| 組成與佈局 | |
| 面的種類 | 2n個五邊形,2個n邊形 |
| 對稱性 | |
| 對稱群 | Dnd, [2+,2n], (2*n), 階數 4n |
| 旋轉對稱群 | Dn, [2,2n]+, (22n), 階數 2n |
| 特性 | |
| 凸 | |
| 註:為底面邊數 。 | |
在幾何學中,截對角偏方面體是一種多面體,可以透過將偏方面體截去上下兩個頂點構成,並具備二面體群對稱性[1]。它的命名方式是根據上下兩個面的形狀而命名的,例如:正十二面體可以視為是截對角正五方偏方面體,它的上下兩個面都是正五邊形,其他的面也是五邊形;[2]:251截對角四方偏方面體的上下兩個面則是正方形或四邊形,其他的面則是五邊形,依此類推。部分的截對角偏方面體可以作為化學的分子籠結構。[3]
形狀
[编辑]截對角偏方面體可以根據其底面邊數分類:
- 截對角三方偏方面體 (杜勒立體):
- 截對角四方偏方面體:
- 截對角五方偏方面體或正十二面體:
- 截對角六方偏方面體:
- ...
- 截對角n方偏方面體:
- 由2n個五邊形和2個n邊形組成,對偶多面體為雙n角錐反角柱。
相關多面體
[编辑]截頂角偏方面體
[编辑]截頂角偏方面體又稱截一角偏方面體是指截去一個頂角的偏方面體。其對偶多面體為角錐反角柱。若截頂角偏方面體的底面邊數為n,則其會有2n+1個面、5n條邊和3n+1個頂點。
| 3 | 4 | 5 | 6 |
|---|---|---|---|
 截頂角三方偏方面體 |
 截頂角四方偏方面體 |
 截頂角五方偏方面體 |
 截頂角六方偏方面體 |
參見
[编辑]參考文獻
[编辑]- ^ Katrina Biele, Yuan Feng, David Heras, Ahmed Tadde. Associating Finite Groups with Dessins d’Enfants (PDF). Purdue Research in Mathematics Experience (PRiME), Department of Mathematics, Purdue University. 2013 [2021-10-23]. (原始内容存档 (PDF)于2021-10-23).
- ^ 2.0 2.1 Alsina, C. and Nelsen, R.B. A Mathematical Space Odyssey: Solid Geometry in the 21st Century. Dolciani Mathematical Expositions. Mathematical Association of America. 2015. ISBN 9781614442165.
- ^ Seong-Pil Kang, Ju-Young Shin, Jong-Se Lim, Sangyong Lee. Experimental measurement of the induction time of natural gas Hydrate and its prediction with polymeric kinetic inhibitor. Chemical Engineering Science. 2014-09, 116: 817–823 [2021-10-07]. doi:10.1016/j.ces.2014.04.035. (原始内容存档于2018-06-09) (英语).
- ^ Weitzel, Hans, A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I, Historia Mathematica, 2004, 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6
- ^ Ziegler, Günter M., Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube, Alex Bellos's Adventures in Numberland, The Guardian, December 3, 2014 [2021-10-23], (原始内容存档于2020-11-11)
- ^ Diudea, M.V. and Nagy, C.L. Diamond and Related Nanostructures. Carbon Materials: Chemistry and Physics. Springer Netherlands. 2013. ISBN 9789400763715.
- ^ Wang, Dong and Cherkaev, Andrej and Osting, Braxton. Dynamics and stationary configurations of heterogeneous foams. PloS one (Public Library of Science). 2019, 14 (4): e0215836.
- ^ Jing Fan, Shin-Hyun Kim, Zi Chen, Shaobing Zhou, Esther Amstad, Tina Lin, David A. Weitz. Creation of Faceted Polyhedral Microgels from Compressed Emulsions (PDF). seas.harvard.edu. [2021-10-23]. (原始内容存档 (PDF)于2021-10-23).
- ^ 9.0 9.1 Wearie-Phelan Bubbles. steelpillow.com. [2019-10-05]. (原始内容存档于2019-08-06).
- ^ Șerban, D. A., Sărăndan, S., Negru, R., Belgiu, G., & Marşavina, L., A Parametric Study of the Mechanical Properties of Open-Cell Kelvin Structures, IOP Conference Series: Materials Science and Engineering 416 (1) (IOP Publishing), 2018, 416 (1): 012108